Borelli (1608-1679) established that the energy that muscle is able to deliver varies in proportion to its volume. And that, for animals of similar build (and so proportion of body volume made up of muscle), all animals should be able to jump the same height in absolute terms. If the muscle work available per body mass m is constant, and the work required to leap a height h against gravity g is mgh (sometimes termed the ‘gravitational potential energy’), then, as work provided by muscle = work required to leap, gh is constant. As g is constant (on Earth, g is about 10 ms^-2), animals of all sizes should be able to lift themselves the same h.

So it is not surprising (and hasn’t been for over 300 years!) that small animals can be remarkably good at leaping in relative terms. And it is entirely mistaken to say that if you scaled a flea to the size of a human it should jump some enormous height.

However, the absolute jump height of small leapers, even clearly specialised fleas and locusts, is not impressive. Henry Bennet-Clark (1977) highlighted the issue of power. Small animals have absolutely short legs; jumping with short legs means leaving the ground in absolutely brief time; a given work in a brief time requires a high power. But peak muscle power is limited, so small animals can’t put as much work in (per body mass), so can’t leap as high. Their adaptations – relatively long legs and catapult elastic mechanisms – can be viewed as partial work-arounds for this problem. But still, the best jumps of the best very small jumpers cannot compete – in absolute terms – with even a jumping human.

The size at which this power problem largely disappears is about that of a gibbon: as shown HERE, gibbons can put in enough energy to jump 3.5m vertically in a single leap, but have long enough legs and arms that this can be applied over a long enough period that the muscles could power this directly (though there is bound to be some elastic recoil too).

Bennet-Clark’s insight that small animals might have problems because of brief periods for muscle action and limited power capability of muscle has wide-ranging implications. Big animals might generally be constrained by the ‘Borelli limit’ of work; small animals by the ‘Bennet-Clark limit’ of instantaneous power. Whenever an animal, especially a small animal, looks like it is doing something uneconomical in terms of mechanical work, consider whether it is ‘buying time’ and reducing the peak power demands.

scaling of posture

In broad terms, small animals tend to be crouched:

And large animals are more upright:

The current textbook account for this HERE focuses on the problems larger animals have in supporting body weight, and proposes that the upright posture of large animals can be attributed to maintaining locomotor stresses within safe limits. However, this does not indicate why small animals should not also be upright, allowing them to benefit from lower locomotor stresses or reduced investment in supporting bones, tendons etc.

THIS PAPER suggests an alternative account, one that applies to both ends of the size scale. It proposes that there is a compromise between postures economical in terms of mechanical work (the relatively stiff, upright postures) and the more compliant postures (leading to more flexed legs) that result in relatively higher stance durations. The flexed postures of small animals effectively ‘buy time’ in order to limit the demand of muscle activation in terms of power at the cost of increased work demand.

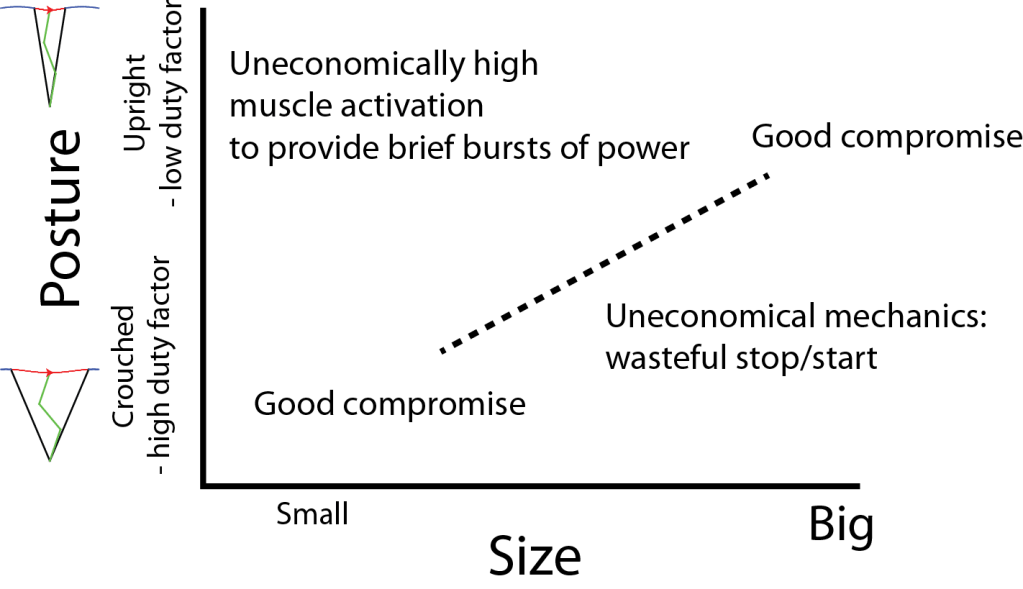
A concept graph from THIS PAPER shows the compromise between work and power that scales with size, resulting in different postures for small and large animals.

scaling of bipedal gaits

Running birds and children have many similarities: if they have an aerial phase, it is minimal (the ‘duty factor’ is about 1/2); and the peak forces occur early in stance.

THIS PAPER and THIS PAPER demonstrate that the peculiar gait of small children (4yrs and under) might be due to their small size and the issues of power generation. A high duty factor and bias of forces early in stance ‘buys’ time for muscle to produce the work, at the cost of demanding a little more work.

scaling of flapping gaits

Geese and many large birds fly steadily with low-amplitude flaps. This flight style is aerodynamically economical as it produces weight-supporting lift by accelerating a large volume (and so mass) of air downwards slowly. Lift depends on the reaction force from giving air a change in momentum (change in mass m x vertical air velocity v) whereas the power demand for this lift is due to the energy given to the air (change in 1/2 mv^2); for a given weight support, it takes less power if a larger mass of air is accelerated.

Small birds tend to fly with large amplitude flaps, and ‘bound’, interspersing periods of flapping with ballistic phases with the wings tucked. This is aerodynamically uneconomical, as a relatively small volume (and so mass) of air is accelerated to support body weight.

THIS PAPER makes the case that the high amplitude flap and bounding flight style reduces the overall costs of activating muscle due to the power demands of flaps over very short periods. And the wings cannot flap too slowly if they are to produce some thrust. The geometry behind this – which also applies to propellers – gives a simple relationship between flight speed, flap amplitude, and frequency, sometimes presented as ‘Strouhal number’ that is necessary for flapping wings – or thrust-producing fins and flukes (expanded on in THIS PAPER). If a volume of muscle has to be activated each flap to achieve the momentary power demand, and this activation is costly in itself, it might as well do alot of work with each contraction (in aerodynamic terms, ‘too much’), even if that means steady, low-amplitude flapping cannot be maintained.

Speed

Why are the fastest animals neither the biggest of the smallest? One answer to this in THIS PAPER is that small animals hit a limit due to the power capacity of muscle (the Bennet-Clark limit), and that big animals are limited by the muscle work capacity (the Borelli limit).